15. ¿En qué consiste la solución de problemas?
La resolución de problemas implica la capacidad de identificar y
analizar situaciones problemáticas cuyo método de solución no resulta
obvio de manera inmediata. Incluye también la disposición a
involucrarnos en dichas situaciones con el fin de lograr nuestro pleno
potencial como ciudadanos constructivos y reflexivos (OCDE, 2014, p. 12)
Paul y Elder(2005).
Resolución de problemas.
Recuperado el 13/08/18 de:
http://www.fod.ac.cr/competencias21/index.php/areas-de-recursos/videos/14-competencias/fichas/68-resolucion-de-problemas#.W3JSHrj6jKQ
16. Planteamiento de solución de problemas según la POLYA.
Definición de problema
Un problema es una situación que ubica a quien lo
resuelve ante la necesidad de desplegar su actividad cognitiva en un
intento de búsqueda de estrategias, de elaboración de conjeturas y toma
de decisiones (Azcue, Diez, Lucanera et al., 2006). En términos
generales, “un problema surge cuando existen obstáculos entre una
situación dada y la situación a la que se quiere llegar, es querer
encontrar un camino para poder llegar del estado actual al estado final,
o al que se quiere obtener” (Torres, 2011, P. 64). El poder ayudar a
que los estudiantes resuelvan problemas debe ser una de las tareas más
importantes del docente de matemáticas. En ese orden de ideas, el
docente debe buscar estrategias para que los estudiantes resuelvan
problemas en diferentes contextos. Con el enfoque del Modelo Pedagógico
del Colegio se pretende que los estudiantes resuelvan problemas a partir
del desarrollo de sus competencias.
Pasos para resolver problemas
Según Ballestero (2002) la solución de problemas
es un complejo constructo, que cumple el doble y poderoso papel de
aliado y/o enemigo en materia de enseñanza, ya que interfiere
directamente en los procesos de enseñanza-aprendizaje, y por tanto en
los niveles de desarrollo alcanzados por el alumno. Generalmente, para
resolver un problema se necesitan de una serie de pasos o procedimientos
heurísticos que, así sea inconscientemente, un individuo debe tener en
cuenta para llegar a la posible solución del mismo (Torres, 2013).
Para los propósitos de este estudio se usará como
referencia el método de cuatro pasos para resolver problemas formulados
por George Polya (1945). De acuerdo con este autor los pasos son: 1.
Entender el problema., 2. Configurar un plan, 3. Ejecutar el plan, y 4.
Examinar la solución.
1. Entender el problema: se
refiere a que el estudiante pueda responderse una serie de preguntas
como ¿Entiendo todo lo que dice el problema?, ¿Puedo replantear el
problema con mis propias palabras?, ¿Cuáles son los datos que hacen
parte del problema?, ¿Sé a dónde quiere llegar?, ¿Hay suficiente
información?, ¿Hay información que no es clara?, ¿Es este problema
similar a algún otro que ya haya resuelto antes?
2. Configurar el plan: se refiere
al cómo o qué estrategia va a usar el estudiante para resolver el
problema. Las estrategias pueden partir desde aplicar pruebas de ensayo y
error, hasta plantear toda una táctica que le permita intentar llegar a
la solución del mismo.
3. Ejecutar el plan: se refiere a
la puesta en práctica de lo que el estudiante estableció en la
configuración. Es llevar a cabo una a una las etapas planteadas. En este
punto puede suceder que en un momento determinado lo que se planteó no
sea pertinente para la solución del problema, razón por la cual hay que
replantear la estrategia y volver a comenzar. Generalmente en la
ejecución se usan procesos matemáticos que permitan darle la exactitud
que requiere la solución del problema.
4. Examinar la solución: se
refiere al poderse cuestionar sobre lo que se hizo, ver si el proceso
desarrollado permitió en realidad resolver el problema. En este paso el
estudiante debe acudir a sus procesos metacognitivos para revisar si lo
que hizo está bien o está mal y, si es necesario, replantear el proceso
de resolución.
Metacongnición
Para Rodríguez (2005), el concepto de metacognición es muy complejo y
reciente en la educación. Dicho constructo se comenzó a trabajar en
procesos de investigación desde la psicología por la década de los
setenta del siglo pasado. La metacognición se ha enmarcado dentro de los
procesos cognitivos en los últimos años y, de acuerdo a Silva (2006),
la metacognición desde la investigación indaga sobre cómo los seres
humanos piensan y controlan sus propios procesos de pensamiento. Curotto
(2010), refiriendo a Flavell (1976), comenta que la metacognición es el
conocimiento sobre los propios procesos y productos cognitivos y el
mismo conocimiento sobre las propiedades de la información, datos
relacionados con el aprendizaje y cualquier aspecto sobre los productos
cognitivos.
Por su parte, Silva (2006) considera que la metacognición tiene dos
clasificaciones y a su vez la primera clasificación se puede asociar a
dos componentes: el conocimiento sobre los procesos cognitivos y la
regulación sobre esos mismos procesos cognitivos. El conocimiento, a su
vez, se encasilla en tres aspectos: el conocimiento sobre el sujeto,
sobre las tareas y sobre las estrategias. De esta forma, lo
metacognitivo se puede encasillar al conocimiento de la amplitud de la
memoria ante tópicos relacionados al conocimiento sobre la complejidad
de las tareas, en donde se establecen jerarquías y se determinan
estrategias para aprendizajes particulares. El segundo componente se
refiere a procesos que permiten regular los procesos metacognitivos. Por
una parte la planificación, actividad que debe ser previa al desarrollo
de cualquier tarea y que según Silva (2006) requiere el diseño de una
heurística para prever el camino de las acciones y estrategias a seguir.
Por otra parte, la actividad establecida en el momento que se comienzan
a ejecutar las acciones, y se traducen a partir de la verificación,
recomposición y revisión de la estrategia empleada. Por último la
evaluación es la que permite constrastar los resultados con los objetivos planteados.
La segunda clasificación que establece Silva (2006) se refiere a dos
líneas de investigación: el monitoreo y el control congnitivo. El
monitoreo se refiere a los procesos de pensamiento y los estados de
conocimiento que hacen parte del individuo. El control metacognitivo es
definidio como la volutad para dirigir los propios procesos de
pensamiento y la recuperación de la memoria. El control combinado con el
monitoreo determinan la planeación y asignación del tiempo al estudio,
el uso de estrategias de aprendizaje y el tiempo necesario para
recuperar alguna información de la memoria. En ese orden de ideas, Silva
(2006) analiza como los procesos metacognitivos de los estudiantes
afectan los procesos de aprendizaje de las matemáticas:
La metacognición es entendida como un componente
del sistema ejecutivo de la inteligencia: nos referiremos al
conocimiento introspectivo sobre el estado de cognición y su operación
la conciencia de lo que uno sabe sobre la manera de cómo lo sabe. Es por
ello que la función de la metacognición es dar forma y regular las
rutinas y estrategias cognitivas (p.81)
Silva (2006) también menciona cómo a medida que la conciencia sobre
lo que está aprendiendo aumenta la actitud frente al conocimiento es más
favorable. Finalmente, este autor afirma que “el aprendizaje es el
resultado de una acción voluntaria por parte de quien aprende”, (p.90)
lo que significa que a mayor conciencia mejor la calidad de lo que se
aprende.
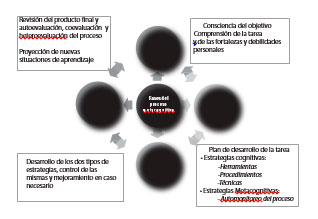
Así mismo, el Modelo Pedagógico del Gimnasio Campestre establece la
metacognición como una de las cuatro competencias que se enseñan,
aprenden y evalúan de manera universal en todos los grados y asignaturas
y se caracteriza a partir de cuatro fases: apropiación de la meta,
planificación de estrategias, desarrollo cognitivo y producto y
evaluación. Estas fases hacen parte de un ciclo, que puede desarrollarse
las veces que sea necesario y exigiendo cada vez más dificultad. En la
figura 1 se observa la interrelación de las fases de la metacognición
desde el Modelo Pedagógico del Gimnasio Campestre (2013).
Teniendo en cuenta lo anterior se pudo establecer una relación entre
la metodología de Polya para la resolución de problemas y lo establecido
desde la competencia de la metacognición en el Modelo Pedagógico del
Gimnasio pestre a partir de los cuatro pasos que cada una maneja (tabla
1).
Materiales y métodos
El enfoque de la investigación fue de carácter cualitativo
interpretativo y el tipo de investigación fue estudio de caso. La
técnica de recolección de la información fue la videoscopía y las
transcripciones, así como la creación de matrices de análisis que
permitieran realizar el seguimiento del proceso de resolución de
problemas de cada uno de los estudiantes, basados en la metodología
propuesta por el matemático húngaro George Polya. Finalmente se
realizaron entrevistas, una antes y otra después del trabajo de campo, a
la docente que desarrolló el trabajo de campo. La unidad de análisis
utilizada fue la sinopsis a partir de cuatro sesiones de clase de 45
minutos cada una.
La población escogida fueron estudiantes de grado quinto en edades
entre 11 y 12 años del Gimnasio Campestre y la muestra fue un total 25
estudiantes.
Et. al. Metodología POLYA en resolución de problemas. Recuperado
el 13/08/18 en:
https://compartirpalabramaestra.org/academia/alianza-gimnasio-campestre-compartir/metodologia-polya-en-resolucion-de-problemas
17. Definición de algoritmo de solución.
ALGORITMOS
DEFINICIÓN:
Un Algoritmo, se puede definir como una secuencia de instrucciones que
representan un modelo de solución para determinado tipo de problemas. O
bien como un conjunto de instrucciones que realizadas en orden conducen a
obtener la solución de un problema. Por lo tanto podemos decir que es
un conjunto ordenado y finito de pasos que nos permite solucionar un
problema.
Los algoritmos son independientes
de los lenguajes de programación. En cada problema el algoritmo puede
escribirse y luego ejecutarse en un lenguaje de diferente programación.
El algoritmo es la infraestructura de cualquier solución, escrita luego
en cualquier lenguaje de programación.
Programa:
Un programa es una serie de instrucciones ordenadas, codificadas en
lenguaje de programación que expresa un algoritmo y que puede ser
ejecutado en un computador.
CLASIFICACIÓN DE ALGORITMOS: Los algoritmos se pueden clasificar en cuatro tipos:
- Algoritmo computacional:
Es un algoritmo que puede ser ejecutado en una computadora. Ejemplo:
Fórmula aplicada para un cálculo de la raíz cuadrada de un valor x.
- Algoritmo no computacional: Es un algoritmo que no requiere de una computadora para ser ejecutado. Ejemplo: Instalación de un equipo de sonido.
- Algoritmo cualitativo:
Un algoritmo es cualitativo cuando en sus pasos o instrucciones no
están involucrados cálculos numéricos. Ejemplos: Las instrucciones para
desarrollar una actividad física, encontrar un tesoro.
- Algoritmo cuantitativo:
Una algoritmo es cuantitativo cuando en sus pasos o instrucciones
involucran cálculos numéricos. Ejemplo: Solución de una ecuación de
segundo grado.
CARACTERÍSTICAS DE UN ALGORITMO: Todo algoritmo debe tener las siguientes características:
- 1. Debe ser Preciso, porque cada uno de sus pasos debe indicar de manera precisa e inequívoca que se debe hacer.
2. Debe ser Finito, porque un algoritmo debe tener un número limitado de pasos.
3. Debe ser Definido, porque debe producir los mismos resultados para las mismas condiciones de entrada.
4. Puede tener cero o más elementos de entrada.
5. Debe producir un resultado. Los datos de salida serán los resultados de efectuar las instrucciones.
PARTES DE UN ALGORITMO: Todo Algoritmo debe tener las siguientes partes:
· Entrada de datos, son los datos necesarios que el algoritmo necesita para ser ejecutado.
· Proceso, es la secuencia de pasos para ejecutar el algoritmo.
· Salida de resultados, son los datos obtenidos después de la ejecución del algoritmo.
TÉCNICAS DE REPRESENTACIÓN:
Para la representación de un algoritmo, antes de ser convertido a
lenguaje de programación, se utilizan algunos métodos de representación
escrita, gráfica o matemática. Los métodos más conocidos son:
· Diagramación libre (Diagramas de flujo).
· Diagramas Nassi-Shneiderman.
· Pseudocódigo.
· Lenguaje natural (español, inglés, etc.).
· Fórmulas matemáticas.

Frida(2009).
Apuntes de informática: Algoritmo. Recuperado el 13/08/18 de: http://informaticafrida.blogspot.com/2009/03/algoritmo.html
18. ¿Qué es un diagrama de flujo?
1.-Definición.-
Un diagrama de flujo es la representación gráfica del flujo o
secuencia de rutinas simples. Tiene la ventaja de indicar la secuencia
del proceso en cuestión, las unidades involucradas y los responsables de
su ejecución, es decir , viene a ser la representación simbólica o
pictórica de un procedimiento administrativo.
Luego,
un diagrama de flujo es una representación gráfica
que desglosa un proceso en cualquier tipo de actividad a desarrollarse
tanto en empresas industriales o de servicios y en sus departamentos,
secciones u áreas de su estructura organizativa.
2.-Objetivo.-

Representar gráficamente las distintas etapas de un proceso y sus
interacciones, para facilitar la comprensión de su funcionamiento. Es
útil para analizar el proceso actual, proponer mejoras, conocer los
clientes y proveedores de cada fase,representar los controles, etc.
3.-Ventajas.-
Podemos citar como ventajas que se pueden obtener con la utilización de los diagramas de flujo, las siguientes:

- Ayudan a las personas que trabajan en el proceso a entender el mismo
, con lo que facilitaran su incorporación a la organización e incluso,
su colaboración en la búsqueda de mejoras del proceso y sus
deficiencias.
- Al presentarse el proceso d una manera objetiva, se permite con
mayor facilidad la identificación de forma clara de las mejoras a
proponer.
- Permite que cada persona de la empresa se sitúe dentro del proceso,
lo que conlleva a poder identificar perfectamente quien es su cliente y
proveedor interno dentro del proceso y su cadena de relaciones, por lo
que se mejora considerablemente la comunicación entre los departamentos y
personas de la organización.
- Normalmente sucede que las personas que participan en la elaboración
del diagrama de flujo se suelen volver entusiastas partidarias del
mismo, por lo que continuamente proponen ideas para mejorarlo.
- Es obvio que los diagramas de flujo son herramientas muy valiosas
para la formación y entrenamiento del nuevo personal que se incorpore a
la empresa.
- Lo mas reseñable es que realmente se consigue que todas las personas
que están participando en el proceso lo entenderán de la misma manera,
con lo que sera mas fácil lograr motivarlas a conseguir procesos mas
económicos en tiempo y costes y mejorar las relaciones internas entre
los cliente-proveedor del proceso.
4.-Elaboración.-
El desarrollo de un diagrama de flujo es una buena herramienta para
ser realizada con un trabajo en equipo, para lo cual se deberán seguir
los pasos que a continuación se exponen:
1
.Se nominan los miembros del grupo de trabajo que deberán elaborar el correspondiente diagrama de flujo del proceso en estudio.
Se elegirán dichas personas entre aquellas que estén participando en
las tareas del proceso, junto a sus proveedores y clientes internos,
ademas de una persona ajena del proceso que , por tanto, sea
independiente del proceso. El objeto de incluir esta persona
independiente se debe a la necesidad de las siguientes premisas:
- Que haga desaparecer la influencia decisiva de algún miembro del grupo en el resultado.
- Que obtenga la participación de todos los miembros del grupo de
trabajo y resuelva los conflictos que pudiera haber, actuando como
moderador .
- Que ayude al grupo a discriminar la información imprescindible de la que no lo es, con objeto de aprovechar mejor el tiempo

2.
Se realizan una serie de reuniones para ir realizando la elaboración de una representación gráfica del proceso
en cuestión. Es importante realizar varias sesiones de trabajo , ya que
así los participantes tendrán mas tiempo para obtener mas información acerca del proceso.
3.Para realizar el diagrama,
los datos son obtenidos a través de un continuo planteamiento de preguntas a los miembros del grupo que se irán repitiendo a lo largo de todo el proceso construcción del diagrama de flujo, como son:
- ¿Que paso es el primero?
- ¿Que paso es el siguiente?
Ademas se deberán utilizar otra serie de preguntas que pueden ayudar a
construir el diagrama en determinadas fases del proceso, a saber:
- ¿De donde viene el servicio o el material?
- ¿Como entra el servicio o material al proceso’
- ¿Quien toma la decisión’
- ¿Que pasa si la decisión es afirmativa SI?
- ¿Que pasa si la decisión es negativa NO?
- ¿Hay algo mas que se deba hacer en este momento del proceso?
- ¿Donde va el producto o servicio de esta operación?
- ¿Que pruebas se realizan al producto en cada fase del proceso?
- ¿Que pruebas se realizan al proceso?
- ¿Que pasa si el producto/servicio no cumple con lo especificado?

4. Todos los datos que se obtengan de las respuestas a las preguntas
mencionadas deberán siendo representadas en hojas del tipo post-it , que
se dejaran bien visibles para todo el grupo de trabajo durante la
realizacion de la confección del diagrama ,
componiendo una especie de mapa mental que ayuda a tomar decisiones.
5. Se deberá
confeccionar una tabla de símbolos estándar
que vayan a ser utilizados normalmente en el diagrama de flujo a
construir. Como ejemplo de los mismos incorporamos una representación
power point con una relación de los mismos.

6.Se recomienda
empezar dibujando el diagrama de flujo mas general del proceso para posteriormente ir detallando mas
cada uno de los diferentes pasos con aquellas características que nos
interesen mas resaltar , como: responsabilidades, archivos, tiempos,
documentación asociada, avisos,etc.. A veces
se suelen incorporar imágenes que ayuden a visualizar
con mas claridad lo que se propone representar. En definitiva, en el
diagrama de flujo se deberá poner todos aquellos elementos que nos den
una mayor información valida para realizar un proceso.

5.-Fases.-
- Definir el proceso y concretar su alcance ( su inicio y final )
- Representar las etapas intermedias y su relación ( proceso actual)
- Documentar cada una de las etapas: Responsable/ Proveedor y Cliente
- Analizar el proceso actual desde el punto de vista deseado.
- Proponer alternativas y definir las nuevas etapas y sus relaciones
- Representar el diagrama del nuevo proceso e indicar las diferencias con el actual.
 6.-Reglas.-
6.-Reglas.-
- Utilizar una simbiologia simple y conocida por los implicados en el proceso.
- Consensuar tanto el diagrama del proceso actual como del nuevo.
- Analizar las implicaciones colaterales de los cambios a introducir.
Miguel, M (2011).
DIAGRAMAS DE FLUJO: su definición, objetivo, ventajas, elaboración, fases, reglas y ejemplos de aplicaciones. Recuperado
el 13/08/18 en:
http://www.luismiguelmanene.com/2011/07/28/los-diagramas-de-flujo-su-definicion-objetivo-ventajas-elaboracion-fases-reglas-y-ejemplos-de-aplicaciones/